Logistic Regression

Introduction

Logistic regression is a parametric classification method that is used to estimate binary class output given real-valued input vectors. In this post, cross entropy loss is used as the loss function and gradient descent (or batched gradient descent) is used to learn parameters.

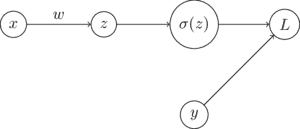
The computation graph below shows how logistic regression works. The dot product of each input, a vector $\vec{x}$ of size $D$, and weight vector $\vec{w}$ transposed is taken, resulting in $z$. $z$ is put through the sigmoid function, and the loss is calculated using the mean squared error on label $y$ and $\sigma(z)$.

The bias term $\beta$ is ignored for the purposes of this post, but can easily be appended to weight vector $\vec{w}$ after appending a $1$ to an input vector $\vec{x}$.

Learning

Given a data set $X$ of size $N$ with $D$ dimensions, parameters $w$ must be learned that minimize our loss function $L_{CE}(y, \hat{y})$. The weight vector is learned using gradient descent. The derivation for term $\frac{\partial L}{\partial w}$ in the weight update is displayed in the derivations section of this post.

$$\begin{aligned} \sigma(z) &= \frac{1}{1 + e^{-z}} & \text{[Logistic function]}\\ L_{\text{CE}}(y, \hat{y}) &= -\left[ y\log \hat{y} + (1-y)\log(1-\hat{y}) \right]& \text{[Cross entropy loss]}\\ w_i &= w_i - \alpha \frac{\partial L}{\partial w_i} & \text{[Weight update]}\\ &= w_i - \alpha \left[x_i (\sigma(z) - y)\right] &\\ w_i &= w_i - \alpha \frac{1}{B}\sum^B_{j=1}x_{j,i}(\sigma(z)-y) & \text{[Batch weight update]}\\ \end{aligned}$$

Code

Code for a logistic regression classifier is shown in the block below

from typing import List from tqdm import trange import torch def ErrorRate(y: torch.Tensor, yhat: torch.Tensor) -> float: """ Calculate error rate (1 - accuracy) Args: y: true labels yhat: predicted labels Returns: error rate """ return torch.sum((y != yhat).float()) / y.shape[0] class LogisticRegressionClassifier: def __init__(self) -> None: """ Instantiate logistic regression classifier """ self.w = None self.calcError = ErrorRate def fit(self, x, y, alpha=1e-4, epochs=1000, batch=32) -> None: """ Fit logistic regression classifier to dataset Args: x: input data y: input labels alpha: alpha parameter for weight update epochs: number of epochs to train batch: size of batches for training """ self.w = torch.rand((1, x.shape[1])) epochs = trange(epochs, desc='Error') for epoch in epochs: start, end = 0, batch for b in range((x.shape[0]//batch)+1): hx = self.probs(x[start:end]) dw = self.calcGradient(x[start:end], y[start:end], hx) self.w = self.w - (alpha * dw) start += batch end += batch hx = self.predict(x) error = self.calcError(y, hx) epochs.set_description('Err: %.4f' % error) def probs(self, x: torch.Tensor) -> torch.Tensor: """ Determine probability of label being 1 Args: x: input data Returns: probability for each member of input """ hx = 1 / (1 + torch.exp(-torch.einsum('ij,kj->i', x, self.w)))[:, None] return hx def predict(self, x: torch.Tensor) -> torch.Tensor: """ Predict labels Args: x: input data Returns: labels for each member of input """ hx = self.probs(x) hx = (hx >= 0.5).float() return hx def calcGradient(self, x: torch.Tensor, y: torch.Tensor, hx: torch.Tensor) -> torch.Tensor: """ Calculate weight gradient Args: x: input data y: input labels hx: predicted probabilities Returns: tensor of gradient values the same size as weights """ return torch.sum(x * (hx - y), dim=0) / x.shape[0]

Derivations

Derivative of loss function $L$ with respect to sigmoid output $a=\sigma(z)$:

$$\begin{aligned} \frac{\partial L}{\partial a} &= \frac{\partial}{\partial a} - \left[y\log a + (1-y) \log (1-a)\right]\\ &= - \left[ y\frac{\partial}{\partial a}\log a + (1-y)\frac{\partial}{\partial a}\log (1-a) \right]\\ &= - \left[ \frac{y}{a}\frac{\partial}{\partial a}a + \frac{(1-y)}{(1-a)}\frac{\partial}{\partial a}(1-a) \right]\\ &= -\left[\frac{y}{a} - \frac{(1-y)}{(1-a)}\right] \end{aligned}$$

Derivative of sigmoid function $\sigma(z)$ with respect to sigmoid input $z$:

$$\begin{aligned} \frac{\partial \sigma(z)}{\partial z} &= \frac{\partial}{\partial z}\frac{1}{1 + e^{-z}}\\ &= \frac{\partial}{\partial z}(1 + e^{-z})^{-1}\\ &= -(1 + e^{-z})^{-2}\frac{\partial}{\partial z}(1 + e^{-z})\\ &= -(1 + e^{-z})^{-2}\frac{\partial}{\partial z}(e^{-z})\\ &= \frac{-e^{-z}}{(1 + e^{-z})^{2}}\frac{\partial}{\partial z}(-z)\\ &= \frac{e^{-z}}{(1 + e^{-z})^{2}}\\ &= \frac{e^{-z}}{1 + e^{-z}} \frac{1}{1 + e^{-z}}\\ &= \left( \frac{1 + e^{-z}}{1 + e^{-z}} - \frac{1}{1 + e^{-z}} \right)\frac{1}{(1 + e^{-z})}\\ &= (1 - \sigma(z))\sigma(z)\\ \end{aligned}$$

Derivative of linear combination $z$ with respect to weight $w_i$:

$$\begin{aligned} \frac{\partial z}{\partial w_i} &= \frac{\partial}{\partial w_i} \sum^D_{j=1}w_j \times x_j\\ &= x_i \end{aligned}$$

Derivative of loss function $L$ with respect to weight $w_i$:

$$\begin{aligned} \frac{\partial L}{\partial w_i} &= \frac{\partial z}{\partial w_i} \frac{\partial \sigma(z)}{\partial z} \frac{\partial L}{\partial \sigma(z)}\\ &= x_i \left[(1-\sigma(z))\sigma(z)\right]\left[\frac{1-y}{1-\sigma(z)}-\frac{y}{\sigma(z)}\right]\\ &= x_i [(1-y)\sigma(z) - (1-\sigma(z))y] \\ &= x_i [\sigma(z)-y\sigma(z) - y + y\sigma(z)] \\ &= x_i [\sigma(z)- y] \\ \end{aligned}$$

Resources

• Jurafsky, Daniel, and James H. Martin. Speech and Language Processing: An Introduction to Natural Language Processing, Computational Linguistics, and Speech Recognition. Pearson, 2020.
• Russell, Stuart J., et al. Artificial Intelligence: A Modern Approach. 3rd ed, Prentice Hall, 2010.